Цель: обобщить знания учащихся по данной теме, их умения и навыки применять формулы.
Задачи:
· образовательные:
- закрепить умение применять формулы квадрата суммы и разности двух выражений;
- ликвидировать возможные пробелы.
· воспитательные:
- вовлечь в активную деятельность всех учащихся класса;
- воспитывать у учащихся любознательность;
- воспитывать коммуникативную культуру общения.
· развивающие:
- развивать познавательный интерес, логическое мышление и мыслительные операции: анализ, сравнение, обобщение, выдвижение гипотезы;
- развивать навыки коллективной работы учащихся в сочетании с самостоятельным умением анализировать, выделять главное, обобщать и делать выводы;
- развивать умение выступать и защищать свою точку зрения.
Тип урока: повторительно-обобщающий.
Оборудование: смарт доска, презентация «Квадрат суммы и квадрат разности», набор разноцветных геометрических фигур (квадратов и прямоугольников), доклад "Треугольник Паскаля".
Ход урока:
I. Организационный момент
Сегодня на уроке мы обобщим наши знания по теме “Квадрат суммы и разности двух выражений”. Вы покажете свои знания формул и умение ими пользоваться. А в конце урока каждый из вас оценит свой труд, насколько хорошо он знает эти формулы и действительно ли умеет ими пользоваться.
В XIX веке в Англии жил известный философ Герберт Спенсер. Он говорил: “Дороги не те знания, которые откладываются в мозгу, как жир; дороги те, которые превращаются в умственные мышцы”. Вот мы сейчас и будем наращивать умственные мышцы.
II. Актуализация знаний.
1. Вводное повторение основных определений темы в виде игры «Домино». Учащимся предлагается собрать имя известного древнегреческого философа математика, сопоставив формулы с их названием. Проговорить формулировки формул.
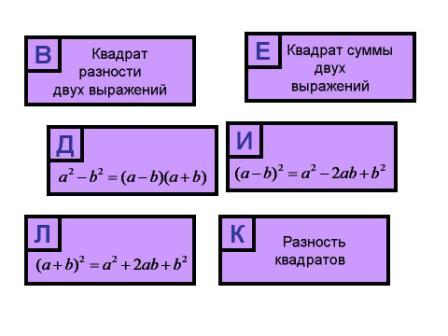
2. Вводное повторение формул.
1) А знаете ли вы, что древнегреческий философ Евклид еще за три века до нашей эры умел возводить в квадрат сумму двух выражений. Вот что писал Евклид в своей замечательной книге «Начала» по поводу одного из математических утверждений: «Если отрезок как-либо разбит на два отрезка, то площадь квадрата, построенного на всем отрезке, равна сумме площадей квадратов, построенных на каждом из двух отрезков, и удвоенной площади прямоугольника, сторонами которого служат эти два отрезка» Неправда ли, что суть этой фразы в формуле: (а + b)2 = a2+ 2ab+ b2.
(Работа по группам)
1 группа (слабые ученики). Выбрать две группы учащихся по два человека в каждой. Им предлагается параллельно с работой класса самостоятельно из разноцветных геометрических фигур (прямоугольников и квадратов) сложить геометрические иллюстрации доказательств формул квадрата суммы и квадрата разности. Двое учащихся работают у смарт доски.

2 группа. Доказывают истинность формул. (№ 807).
I вариант. № 807 (а): (a – b)2 = (b – a)2.
II вариант. № 807 (б): (– a – b)2 = (a + b)2.
По одному человеку от каждого варианта на доску, доказывать формулу.
Таким образом, мы получили три способа формулировки математических утверждений:
1) словесный – понятный, но длинный, неудобный;
2) геометрический – наглядный, но не всегда удобный для вычислений;
3) символьный – краткий, легко запоминающийся.
2) Проверка знаний формул.
Проверьте решение. Если решение выполнено верно, поставьте рядом знак плюс, если нет – поставьте знак минус.

Взаимопроверка. Поменяться тетрадями с соседом по парте.
III. Закрепление изученного материала.
Математик А.Н. Крылов говорил, что «рано или поздно всякая правильная математическая идея находит применение в том или ином деле».
В формулах квадрата суммы и квадрата разности, в квадрат возводят сумму или разность двух выражений. Еще Евклид знал прием возведения в квадрат суммы двух слагаемых. Но почему только двух? И почему только в квадрат? Может быть, можно найти прием возведения в 3, 4 и более высокие степени суммы трех, четырех и более чисел? Оказывается, нетрудно получить формулы для возведения двучлена в третью, четвертую и т. д. степень.
Доклад «Треугольник Паскаля»


А если надо возвести в квадрат сумму трех слагаемых? Каким будет результат? Предположим, что он выглядит так:
(a + b + c)2 = a2 + b2 + c2 + 2ab + 2ac + 2bc.
Предложите свой способ решения.
(a + b + c)2 = ((a + b) + c)2 = (a + b)2 + 2(a + b)c + c2 = a2 + 2ab + b2 + 2ac + 2bc + c2 = a2 + b2 + c2 + 2ab + 2ac + 2bc
Вывод: Значит, чтобы возвести в квадрат сумму трех слагаемых, опять использовали формулу квадрата суммы двух выражений.
IV. Физкультминутка.
1. Потереть ладонью о ладонь. Закрыть глаза и положить на них ладони. Отдых 10 – 15 с.
2. Быстро поморгать глазами. Закрыть глаза. Отдых 10 – 15 с.
3. Открыть глаза.
V. Закрепление изученного материала.
А теперь мы продолжим работу.
1) Представьте в виде квадрата двучлена:
I вариант: а) (2а + 3b)2 – 8b(2а + b)
II вариант: б) (3х – 2у)2 + 5х(4у – х)
2) Как вычислить квадрат числа, оканчивающегося на 5? Гипотезы.
Любое число, оканчивающееся на 5, можно представить в виде:
(10n+5), где n – число десятков
Возведём в квадрат: 100n2+100n+25
Вынесем общий множитель за скобку: 100n(n+1)+25
Пример: 252 = 625, 752 = 5625, 1152 = 13225
3) Пришла пора проверить, как обстоят дела с наращиванием умственных мышц.
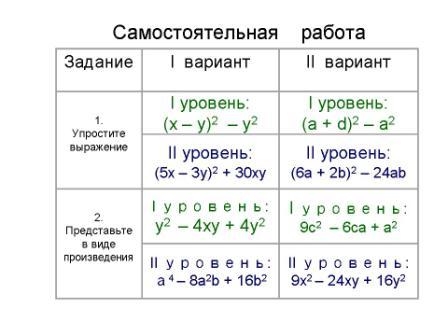

(Ученики сдают тетради на проверку. На доске появляются ответы и ученики проверяют.)
VI. Итог урока.
Сегодня на уроке мы обобщили наши знания по теме “Квадрат суммы и разности двух выражений”. Каждый из вас получил оценку за свой труд, насколько хорошо он знает эти формулы и действительно ли умеет ими пользоваться.
С помощью формул можно доказывать интересные математические утверждения, которые в математике получили название «Софизмы». Вот один из них.
“Неравные числа равны”
Возьмем два неравных между собой произвольных числа а и b. Пусть их разность равна с, т. е. а – b = с. Умножив обе части этого равенства на а – b, получим
(а– b)2 = = c(a – b),
a раскрыв скобки, придем к равенству
a2 – 2ab + b2 = = ca – cb,
из которого следует равенство
а2 – аb – ас = аb – b2 – bc.
Вынося общий множитель а слева, и общий множитель b справа за скобки, получим
а(а – b – с ) = b(а – b – с). (1)
Разделив последнее равенство на (а – b – с), получаем, что а = b,
другими словами, два неравных между собой произвольных числа а и b равны.
Разбор софизма: Здесь ошибка совершена при переходе от равенства (1) к равенству а = b. Действительно, согласно условию разность двух произвольных чисел а и b равна с, т. е. а-b = с, откуда а – b – с = 0. Можно записать равенство (1) в виде а – 0 = b – 0. Переход от равенства (1) к равенству а = b осуществляется путем деления обеих частей (1) на равное нулю число а – b – с = 0. Следовательно, здесь мы имеем деление нуля на нуль, которое не имеет смысла, поскольку равенство а*0 = b*0 выполняется при любых а и b. Поэтому вывод, сделанный в софизме, что числа а и b равны, неверен.
Вывод: Мы готовы на следующем уроке приступить к изучению новой темы.
VII. Домашнее задание.
На оценку «3» № 878, 879(а,б), 903
На оценку «4,5» №878, 879, 903
VIII. Рефлексия
Продолжите фразу: «Я на уроке научился (или узнал) …».
Источники:
1. Алгебра: учеб. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев и др; Под ред. С.А. Теляковского. – М.: «Просвещение», 2012.
2. Алгебра. Дидактические материалы. 7 класс / Л. И. Звавич, Л. В. Кузнецова, С. Б. Суворова. — М.: «Просвещение», 2012.
3. Блез Паскаль. Сайт ВикипедиЯ: https://ru.wikipedia.org/wiki/%CF%E0%F1%EA%E0%EB%FC,_%C1%EB%E5%E7.
4. Лобанова И.С. «Обобщающий урок по алгебре в 7-м классе по теме «Возведение в квадрат суммы и разности двух выражений». Сайт Фестиваля «Открытый урок»: http://festival.1september.ru/articles/513801/.
|