Цель: формировать умение читать и строить график функции, заданной аналитически.

Задачи:

• образовательные:

- сформировать понятие «график функции»;

- обучить читать и строить график  функции,  заданной  аналитически;

- познакомить учащихся с различными графиками и отраслями знаний, в которых они могут быть использованы;

• воспитательные:

- воспитывать у учащихся аккуратность, наблюдательность, любознательность и положительную мотивацию к учению;

• развивающие:

- расширять познавательный интерес и кругозор учащихся;

- развивать речь, графические навыки, умение анализировать полученные результаты;

-  развивать межпредметные связи между математикой и другими науками.

Тип урока: комбинированный урок с использованием мультимедиа технологий.

Список используемого программного обеспечения и готовых электронных образовательных ресурсов: компьютер (ноутбук) с выходом в сеть Интернет, кроссворд «Функция» на сервисе: http://puzzlecup.com/crossword-ru/?guess=997C7969B53A4C52 , тест «Что такое функция. Вычисление значений функций по формуле» на сервисе: http://www.slideboom.com/presentations/626996/Tect-Funkzia, программа для построения графиков функций, доклад «Применение графиков функций» на сервере:  http://youtu.be/lFuH-ERc0bw, творческая работа «Функции в пословицах и поговорках» http://en.calameo.com/read/0016676558c9b2b218acb.

Ход урока

1. Организационный момент

2. Постановка цели и мотивация

Как заметил Г. Галилей, книга природы написана на математическом языке и её буквы - математические знаки и геометрические фигуры - невозможно понять её слова. И именно функция является тем средством математического языка, которое позволяет описывать процессы движения, изменения, присущие природе. [4]

Впервые функция вошла в математику под именем «переменная величина» в знаменитом труде французского математика и философа Р. Декарта «Геометрия» (1637 г.). С развитием науки понятие функции уточнялось и обобщалось.

3. Актуализация опорных знаний

Кроссворд «Функция». Фронтальная работа с классом. Проверка знаний формулировок, определений, правил по теме «Функция».

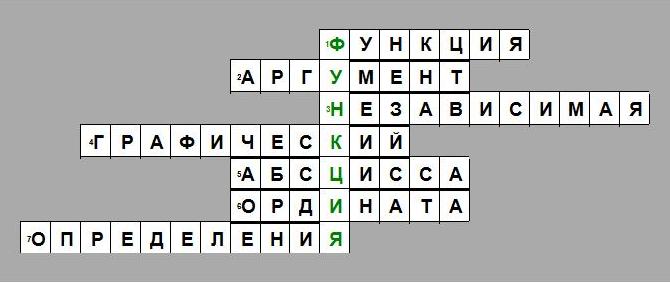
По горизонтали: 1. Зависимая переменная.   2. Независимая переменная.  3. Переменная, значение которой выбирают произвольно.   4. Способ задания функции.   5. Название координаты х на координатной плоскости.   6. Название координаты у на координатной плоскости.  7. Как называется область функции, которую образуют все значения независимой переменной.  

По вертикали: 1. Зависимость одной переменной от другой.  

4. Проверочная работа

С помощью теста «Что такое функция. Вычисление значений функций по формуле» проверяется на сколько усвоен учебный материал. Учащиеся самостоятельно выполняют задания теста, затем происходит взаимопроверка, учащиеся обмениваются с соседом тетрадями.

5. Объяснение нового материала

1) Формирование представления о графике функции на основе связи аналитического, табличного и графического способов задания функции.

Учитель: На предыдущих уроках мы уже познакомились с основными способами задания функции. Особое внимание было уделено связи аналитического и табличного способов. На этом уроке наша задача – показать, что эти два способа тесно связаны с графическим, причем его особенность в том, что с помощью графика мы можем наглядно представлять функциональную зависимость не только для точечной, но и бесконечной области определения функции:

2) Построение графика функции по точкам.

Учитель: Функция задана формулой  у = х(х – 3),  где – 2 < х < 2. Заполните таблицу.

Построить график, соединив эти точки плавной линией. (см. № 283)

Необходимо  сделать  вывод:  по  точкам  можно  построить  график любой  функции,  заданной  таблично  или  аналитически  (с  помощью формулы).

3) введение определения понятия графика функции

Физкультминутка (упражнения для глаз):

1. Закрыть глаза. Отдых 10—15 с. Открыть глаза. Повторить 2-3 раза.

2. Закрывать и открывать глаза, крепко сжимая веки. Повторить 5-6 раз.Закрыть глаза, расслабить веки, 10—15 с.

3. Быстро поморгать глазами. Закрыть глаза. Отдых 10—15 с. Открыть глаза.

4) Работа по изображенному графику функции.

Пример 2 с. 60 учебника изучаем работу по изображенному графику на нахождение значения функции по заданному значению аргумента и обратное задание.

Работа по графику из № 283, вопросы:

а) Сколько точек пересечения с осью х имеет график? Каково значение у в этих точках?

б) Сколько точек пересечения с осью у имеет график? Каково значение х в этой точке?

в) Сравните значения функции в точках –2 и 1.

г) Назовите координаты какой-нибудь точки графика, у которой значения аргумента и функции положительны; значение аргумента положительно, а функции – отрицательно и т. д.

5) Презентация творческой работы «Применение графиков функций».

Учащийся (группа учащихся) представляют презентацию «В каких же отраслях знаний могут быть использованы графики?»

6. Формирование умений и навыков

1. № 284

2. № 285 (1 вариант - рис. 15, 2 вариант - рис. 16), двое учащихся работают у доски.

7. Итоги урока

Вопросы для учащихся:

– Что называется графиком функции?

– Как построить график функции, заданной формулой?

– Как по графику найти значение функции, соответствующее данному значению аргумента?

– Как по графику функции найти значение аргумента, которому соответствует данное значение функции?

- Как по графику зависимости определить, является ли она функцией?

8. Рефлексия

Закончи предложение:

Что узнали, изучив тему…

Чему научились, изучив тему…

Какие испытали трудности…

9. Домашнее задание:

1. п. 14, определение, № 286 – 288

2. Творческое задание: проект «Функции в пословицах и поговорках». (Показать примеры).

Литература:

1. Алгебра: учеб. для 7 кл. общеобразоват. учреждений / Ю.Н. Макарычев и др; Под ред. С.А. Теляковского. – М.: «Просвещение», 2011г.

2. Алгебра. 7 класс: поурочные планы по учебнику Ю.Н. Макарычева и др. (компакт-диск) – издательство «Учитель», 2011.

3. Глазков Ю.А. Самостоятельные и контрольные работы по алгебре: 7 класс: к учебнику Ю.Н. Макарычева и др.   – М.: Издательство «Экзамен», 2011.

4. Шмутцер Э., Шютц В. Галилео Галилей. — М.: Мир, 1987. — С. 116.